Pensez au déjeuner. Peut-être un bon sandwich au jambon. Un coup de couteau coupe soigneusement le jambon et ses deux tranches de pain. Mais que se passe-t-il si vous glissez ? Oups, le jambon repose désormais plié sous une assiette retournée, avec une tranche de pain au sol et l’autre collée au plafond. Voici un peu de réconfort : la géométrie garantit qu’une seule coupe droite, peut-être à l’aide d’une machette de la taille d’une pièce, peut toujours couper parfaitement les trois morceaux de votre déjeuner roulé, laissant exactement la moitié du jambon et la moitié de chaque tranche de pain de chaque côté du couper. En effet, le « théorème du sandwich au jambon » promet que pour trois objets (potentiellement asymétriques) dans n’importe lequel orientation, il y a toujours une coupe droite qui les coupe tous simultanément. Ce fait a des implications bizarres ainsi que des implications qui donnent à réfléchir en ce qui concerne charcuterie en politique.
Le théorème se généralise également à d’autres dimensions. Une formulation plus mathématique dit que n objets dans n-l’espace dimensionnel peut être simultanément divisé en deux par un (n – 1)–coupe dimensionnelle. Ce sandwich au jambon est un peu long, mais nous allons le rendre plus digeste. Sur une feuille de papier en deux dimensions, vous pouvez dessiner n’importe quoi deux formes que vous voulez, et il y aura toujours une ligne droite (unidimensionnelle) qui coupe parfaitement les deux en deux. Pour garantir une coupe égale pour trois objets, nous devons passer à trois dimensions et les couper avec un plan bidimensionnel : imaginez cette machette qui ravage la pièce comme glissant un mince morceau de papier entre les deux moitiés de la pièce. En trois dimensions, la machette a trois degrés de liberté : vous pouvez la balayer d’avant en arrière à travers la pièce, puis l’arrêter et la faire pivoter sous différents angles, et alors aussi balancez la machette d’un côté à l’autre (comme la façon dont les carottes sont souvent coupées obliquement et non droites).
Si vous pouvez imaginer un sandwich au jambon en quatre dimensions, comme mathématiciens que vous aimez faire, vous pouvez également diviser un quatrième ingrédient en deux avec une coupe en trois dimensions.
Sur le soutien au journalisme scientifique
Si vous appréciez cet article, pensez à soutenir notre journalisme primé en s’abonner. En achetant un abonnement, vous contribuez à assurer l’avenir d’histoires percutantes sur les découvertes et les idées qui façonnent notre monde d’aujourd’hui.
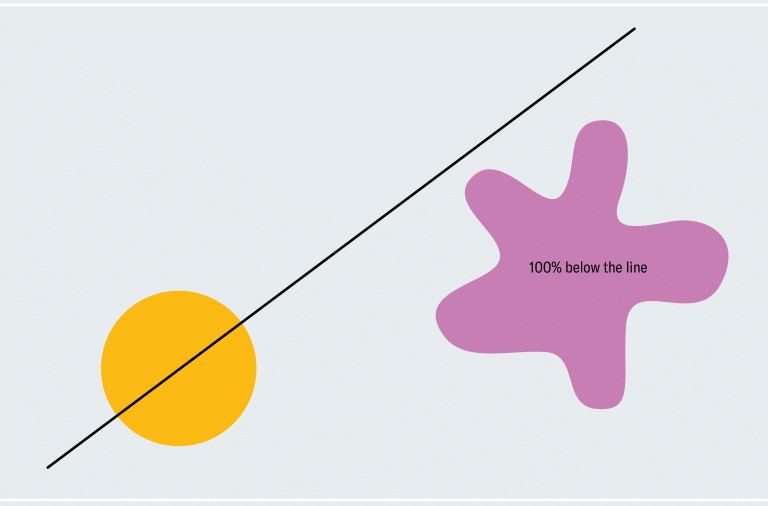
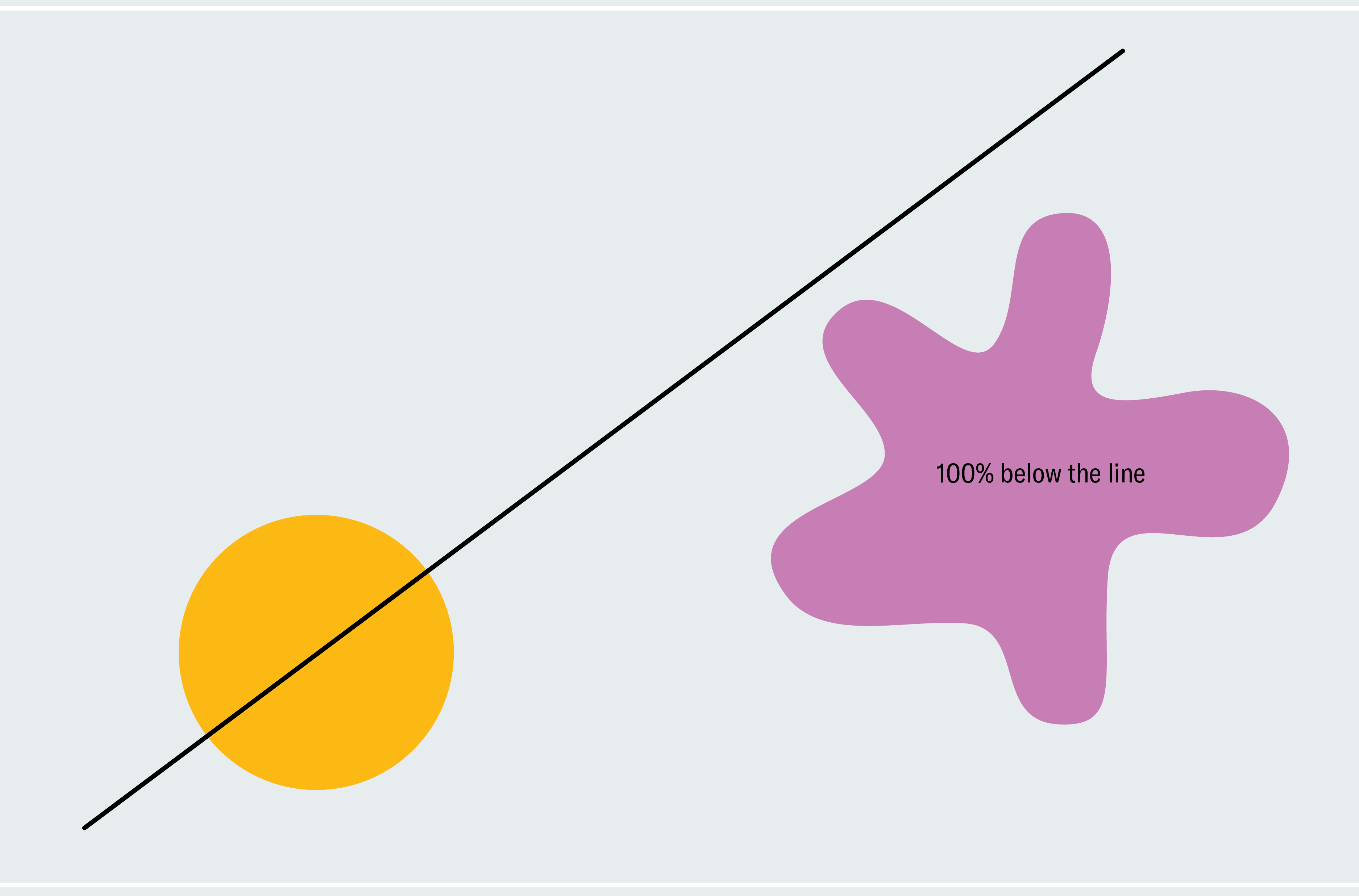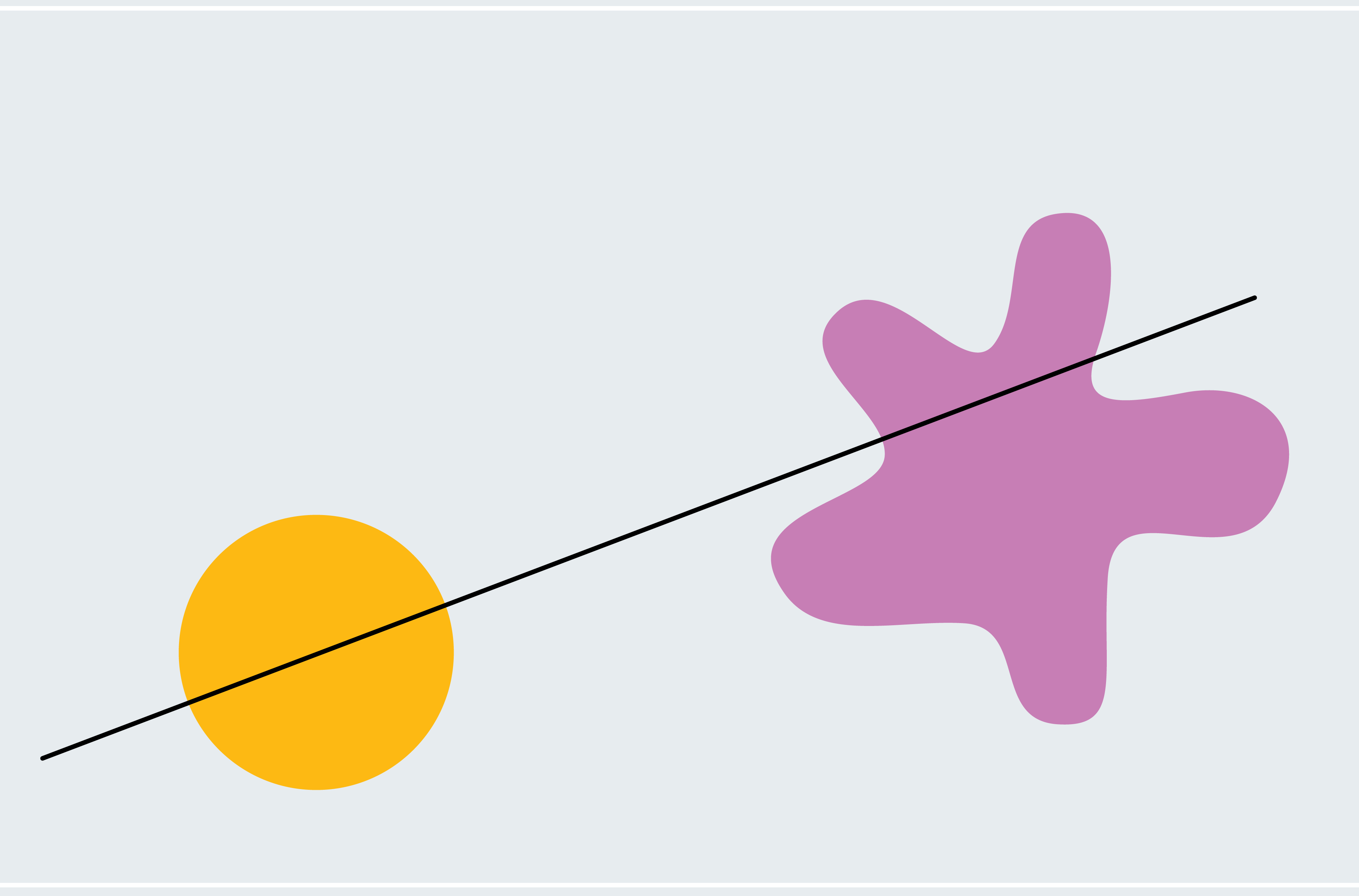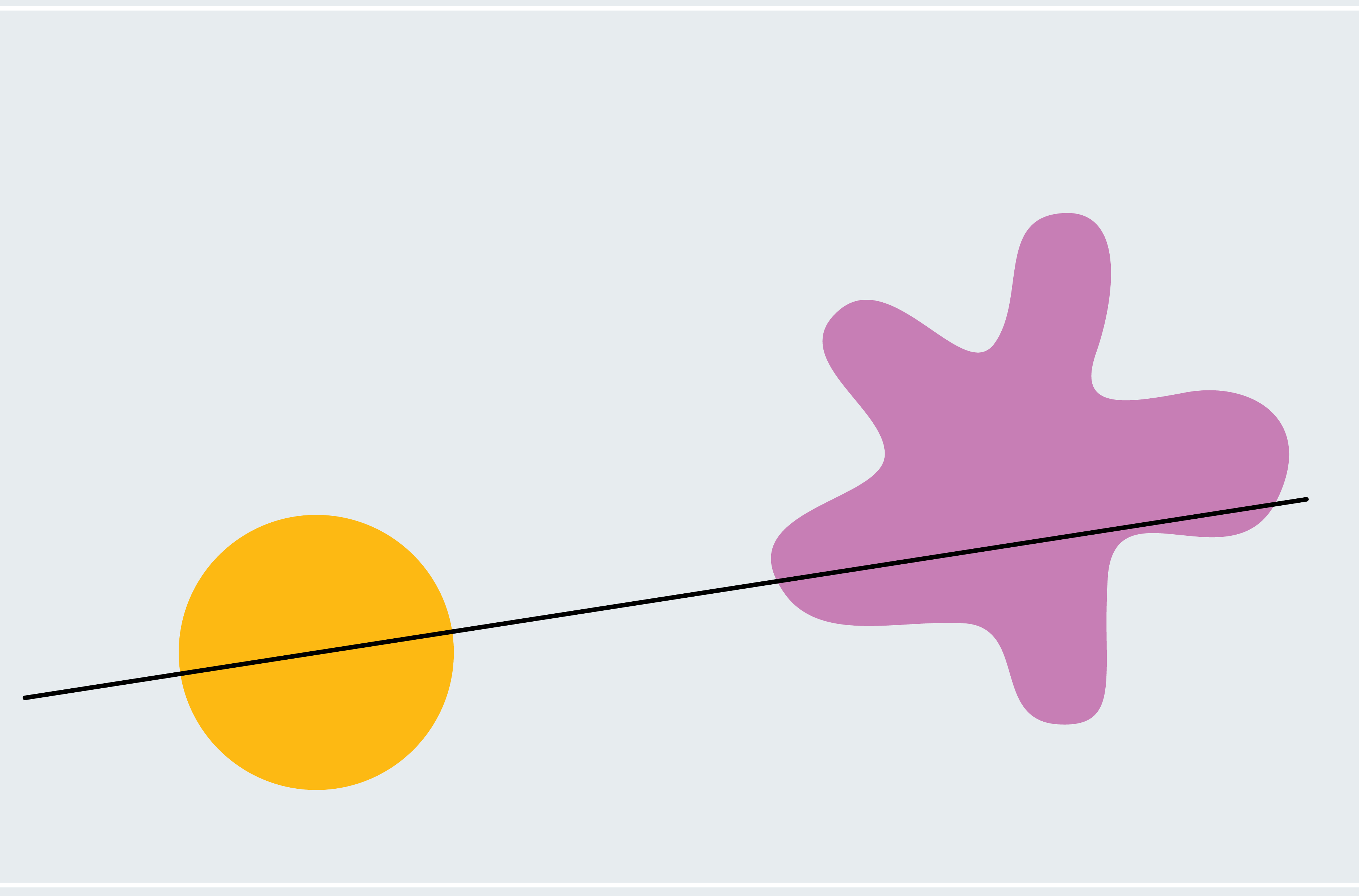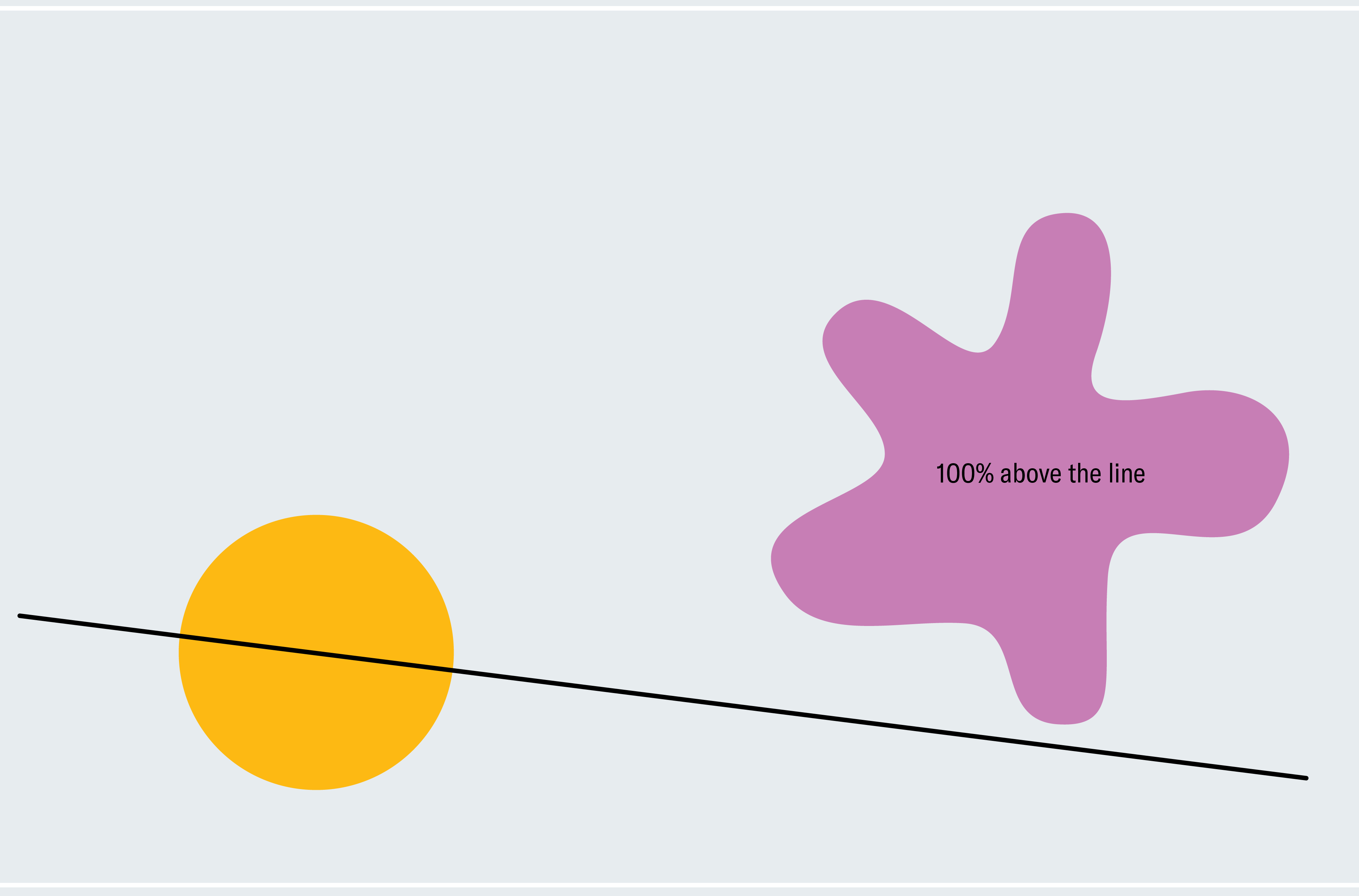
Pour avoir une idée de la façon de prouver le théorème du sandwich au jambon, considérons une version simplifiée : deux formes en deux dimensions, l’une d’elles étant un cercle et l’autre une goutte. Chaque ligne qui passe par le centre d’un cercle le coupe en deux (les formes asymétriques n’ont pas nécessairement un centre comme celui-ci ; nous utilisons un cercle pour nous faciliter la vie pour l’instant). Comment savons-nous que l’une de ces lignes coupe également la goutte en deux ? Choisissez une ligne passant par le centre du cercle qui ne coupe pas du tout la goutte. Comme le montre le premier panneau ci-dessous, 100 % de la goutte se trouve en dessous de la ligne. Maintenant, faites pivoter lentement la ligne autour du centre du cercle comme un moulin à vent. Finalement, il franchit la goutte, la traverse de plus en plus, puis passe en dessous, là où zéro pour cent de la goutte se trouve en dessous de la ligne. De ce processus, nous pouvons déduire qu’il doit y avoir un moment où exactement 50 % de la goutte se trouve en dessous de la ligne. Nous passons progressivement de 100 % en continu à zéro %, nous devons donc transmettre chaque montant intermédiaire, ce qui signifie qu’à un moment donné, nous sommes exactement à 50 % (fans de calcul pourrait reconnaître cela comme le théorème des valeurs intermédiaires).
Cet argument prouve qu’il existe une ligne qui coupe simultanément nos formes (bien qu’il ne nous dise pas où se trouve cette ligne). Cela repose sur le fait que chaque ligne passant par le centre d’un cercle le coupe en deux, ce qui nous permet de faire pivoter librement notre ligne et de nous concentrer sur la goutte sans craindre de négliger le cercle. Deux formes asymétriques nécessitent une version plus subtile de notre technique de moulin à vent, et l’extension à trois dimensions implique des arguments plus sophistiqués.
Il est intéressant de noter que le théorème reste vrai même si le jambon et le pain sont brisés en plusieurs morceaux. Utilisez un emporte-pièce pour découper des bonhommes de neige au jambon et faites cuire votre pain en croûtons ; une coupe parfaitement égale existera toujours (chaque bonhomme de neige ou croûton ne sera pas forcément réduit de moitié, mais la quantité totale de jambon et de pain le sera). En poussant cette idée à l’extrême, nous pouvons faire une affirmation similaire sur certains points. Parsemez votre papier de points rouges et verts, et il y aura toujours une ligne droite avec exactement la moitié des rouges et la moitié des verts de chaque côté. Cette version nécessite une petite technicité : les points qui se trouvent exactement sur la ligne de démarcation peuvent être comptés d’un côté ou de l’autre ou ne pas être comptés du tout (par exemple, si vous avez un nombre impair de rouges, vous ne pourriez jamais les diviser uniformément sans cette mise en garde).
Considérez les implications bizarres ici. Vous pouvez tracer une ligne à travers les États-Unis pour qu’exactement la moitié des mouffettes du pays et la moitié de ses barres Twix se trouvent au-dessus de la ligne. Bien que les mouffettes et les barres Twix ne soient pas réellement des points uniques, elles pourraient tout aussi bien l’être par rapport à la vaste toile du territoire américain. En augmentant les choses d’une dimension, vous pouvez dessiner un cercle sur Terre (trancher un globe laisse une section transversale circulaire) qui contient la moitié des roches du monde, la moitié de son papier et la moitié de ses ciseaux, ou toute autre catégorie loufoque de votre choix. .
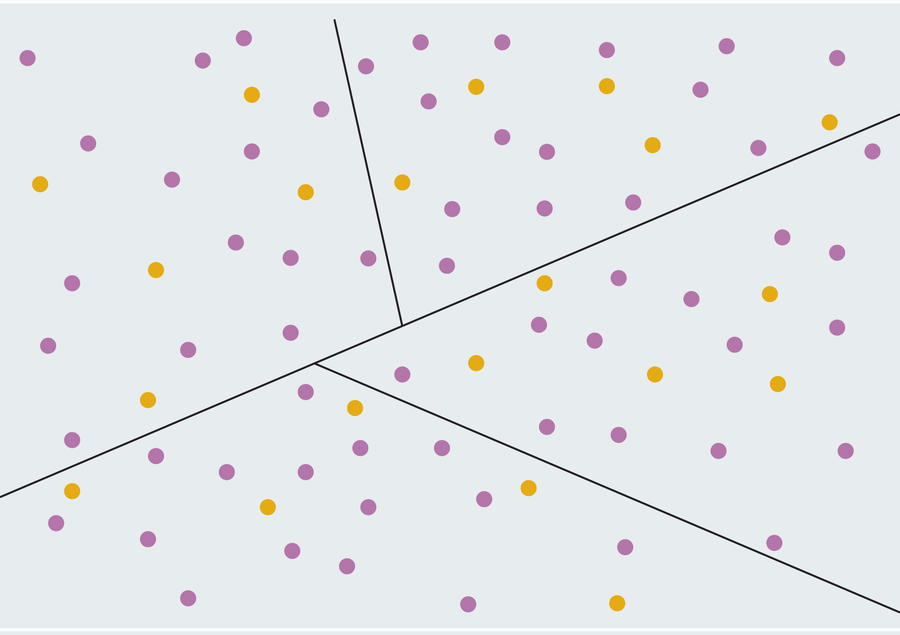
Comme nous l’avons mentionné, le théorème du sandwich au jambon entraîne des conséquences bien moins fantaisistes pour le problème éternel du gerrymandering en politique. Aux États-Unis, les gouvernements des États divisent leurs États en circonscriptions électorales, et chaque circonscription élit un membre à la Chambre des représentants. Le gerrymandering est la pratique consistant à délimiter délibérément ces limites de district à des fins politiques. Pour un exemple simplifié, imaginez un État avec une population de 80 habitants. 75 pour cent d’entre eux (60 personnes) sont favorables au parti violet et 25 pour cent (20 personnes) préfèrent le parti jaune. L’État sera divisé en quatre districts de 20 habitants chacun. Il semble juste que trois de ces districts (75 pour cent) passent au violet et l’autre au jaune afin que la représentation de l’État au Congrès corresponde aux préférences de la population. Cependant, un cartographe astucieux pourrait modifier les limites des circonscriptions de telle manière que chaque circonscription contienne 15 électeurs violets et cinq électeurs jaunes. De cette façon, le parti violet détiendrait la majorité dans chaque circonscription et 100 pour cent de la représentation de l’État proviendrait du parti violet au lieu de 75 pour cent. En fait, avec suffisamment d’électeurs, n’importe lequel Le pourcentage d’avantage qu’un parti possède sur un autre (disons 50,01 pour cent de violet contre 49,99 pour cent de jaune) peut être exploité pour gagner. chaque district; faites simplement en sorte que 50,01 pour cent de chaque district soutienne le parti majoritaire.
Bien entendu, ces quartiers semblent très artificiels. Un moyen apparemment évident de réduire le gerrymandering serait d’imposer des restrictions sur la forme des districts et d’interdire les monstruosités tentaculées que l’on voit souvent sur les cartes électorales américaines. En effet, de nombreux États imposent de telles règles. Même s’il peut sembler qu’exiger que les districts aient des formes « normales » contribuerait grandement à atténuer le problème, intelligent des chercheurs J’ai appliqué un certain théorème géométrique pour montrer à quel point c’est un tas de bêtises. Reprenons notre exemple : 80 électeurs comprenant 60 partisans violets et 20 partisans jaunes. Le théorème du sandwich au jambon nous dit que quelle que soit la manière dont ils sont distribués, nous pouvons tracer une ligne droite avec exactement la moitié des électeurs violets et la moitié des électeurs jaunes de chaque côté (30 violets et 10 jaunes des deux côtés). Traitez maintenant chaque côté de la coupe comme son propre problème de sandwich au jambon, en divisant chaque moitié avec sa propre ligne droite de sorte que chaque région résultante contienne 15 violets et cinq jaunes. Les violets ont désormais le même avantage qu’auparavant (ils gagnent tous les districts), mais les régions qui en résultent sont toutes simples avec des frontières en ligne droite !
La subdivision répétée du sandwich au jambon produira toujours des districts relativement simples (en langage mathématique, ce sont des polygones convexes, sauf là où ils partagent potentiellement une frontière avec une frontière d’État existante). Cela signifie que les réglementations de base sur la forme des circonscriptions du Congrès ne peuvent probablement pas exclure même les pires cas de gerrymandering. Bien que les mathématiques et la politique puissent sembler des domaines lointains, un détournement géométrique inutile nous a appris que la solution la plus naturelle au gerrymandering ne coupe pas la moutarde.