La réponse est simple : c’est parce que le Soleil est l’objet le plus massif du système solaire.
L’attraction gravitationnelle du Soleil est massive puisque le Soleil pèse environ 1,989×1030 kg, pour mettre cela en perspective, le Le soleil contribue à hauteur d’environ 99,8 % de toute la masse du système solaire !
C’est pourquoi elle possède le champ gravitationnel le plus puissant du système solaire, provoquant la rotation d’autres planètes autour d’elle.
Mais la question se pose encore plus lorsque vous essayez de creuser plus loin : si le Soleil a une gravité si forte, pourquoi toutes les autres planètes, y compris la Terre et d’autres objets, ne s’écrasent-elles pas sur le Soleil ? Ou qu’est-ce qu’une orbite exactement ?
Les lois du mouvement et de la gravité de Newton
En commençant par les bases, en mécanique classique, nous traitons la gravité comme une force attractive entre des objets qui ont une masse, et tout objet qui a une certaine masse possède un champ gravitationnel.
Avec le Loi universelle de la gravitation Newton nous a appris que tout objet massif attire tout autre objet autour de lui, ce que l’on appelle la loi de la gravité de Newton. Cela ressemble à ceci :
$$F = – \frac{G m_1 m_2}{r^2}$$
Où $G$ est la constante gravitationnelle universelle, $m_1$ est la masse d’un objet, $m_2$ est la masse d’un autre objet et $r$ est la distance entre les centres des deux objets.
Vous pouvez maintenant considérer que $m_1 = M_{soleil}$ ou la masse du Soleil, et $m_2$ comme étant égal à la masse de tout autre objet du système solaire pour trouver la force gravitationnelle entre eux.
En raison de la force gravitationnelle entre deux objets, ils accélèrent l’un par rapport à l’autre, cependant, le corps ayant la plus grande masse a une plus grande influence sur l’autre.
Disons que nous voulons déterminer l’accélération gravitationnelle sur une planète due à la gravité du Soleil, nous pouvons commencer par ce qui suit :
$$F_{g} = M_{p}\cdot a$$
$$- \frac{G\cdot M_{s}\cdot M_{p}}{r^2} = M_{p}\cdot a$$
$$a = – \frac{GM_{s}}{r^2}$$
Ici, $F_{g}$ est la force de gravité entre la planète et l’objet, $M_s$ et $M_p$ sont respectivement les masses du Soleil et de la planète, $a$ est l’accélération sur n’importe quelle planète due à l’accélération du Soleil. la gravité, et $r$ est la distance qui les sépare.
Nous connaissons donc désormais la force de gravité qui tire tout vers le Soleil, mais qu’est-ce qui empêche la planète de tomber sur le Soleil ?
Qu’est-ce qui empêche les planètes de tomber sur le Soleil ?
Une autre force en action annule l’effet de la gravité provoqué par la nature du mouvement de ces planètes.
Cette force est appelée la force centrifugec’est la raison pour laquelle la corde d’un yoyo s’étire lorsque vous la balancez dans les airs.
Chaque fois qu’un objet effectue un mouvement circulaire, il subit toujours une force extérieure, c’est ce qu’on appelle un force non inertiellece qui signifie simplement qu’il est ressenti comme une force chaque fois que le système de référence tourne lui-même.
C’est ce qu’on appelle la force centrifuge.
Si vous regardez des enfants monter sur le manège, dans votre référence, il n’y a pas de force extérieure, mais lorsque vous montez vous-même sur le manège, ce qui signifie que vous êtes dans le cadre en rotation, vous ressentirez une force vers l’extérieur. forcer.
La force extérieure vous donne l’impression d’être éjecté du manège.
Voici la première loi du mouvement-inertie de Newton à expliquer.
« Un objet au repos restera au repos, et un objet en mouvement restera en mouvement avec une vitesse constante à moins qu’il ne soit soumis à une force externe nette. »
En raison de l’inertie, l’objet concerné veut toujours se déplacer sur une trajectoire rectiligne, mais comme il change tout le temps de direction dans un mouvement circulaire, cela donne la sensation de force qui le tire vers l’extérieur.
Les enfants qui montent sur le manège ne ressentent pas vraiment une force attractive comme la gravité, les tirant vers le centre de la structure du manège.
C’est leur siège relié au centre par une tige, qui les maintient limités à un endroit, et il y a une force de tension sur cette tige, dirigée vers le centre.
Dans le mouvement planétaire, nous avons la gravité du Soleil, que nous traitons comme une force attractive qui attire les planètes vers le Soleil, nous pouvons également l’appeler force centripète dans ce cas.
Étant donné que les planètes effectuent un mouvement circulaire autour du Soleil, elles subissent le même type de force centrifuge vers l’extérieur qui équilibre l’attraction gravitationnelle du Soleil, c’est pourquoi elles tournent autour du Soleil sans tomber dedans.
Cependant, encore une fois, cette force centrifuge n’est pas une force réelle mais résulte de l’inertie et de la vitesse de l’objet dans un mouvement circulaire.
Visualiser les orbites : lancer une balle dans l’espace
Une façon plus amusante d’imaginer ce scénario d’orbite est de supposer que vous lancez une balle, que se passe-t-il ? il parcourt une certaine distance dans les airs et tombe.
Maintenant, lancez le ballon avec plus de force cette fois, et maintenant ? c’est allé plus loin qu’avant.
Essayez de le jeter à quelques kilomètres de là, il ne vous sera peut-être pas physiquement possible de le faire, mais supposons simplement que vous le puissiez.
Essayez de toutes vos forces et lancez-le à 420 kilomètres de hauteur. Est-ce qu’il est tombé ?
Si vous l’avez bien fait, vous le trouverez peut-être en train d’accueillir les astronautes de la Station spatiale internationale, qui orbite également autour de la Terre à 420 kilomètres d’altitude.
Si nous supposons que vous l’avez bien fait, cela signifierait premièrement que la balle a atteint une altitude de 420 kilomètres, deuxièmement, qu’elle avait une trajectoire courbe et troisièmement qu’elle avait une vitesse suffisante, ce qui signifie qu’elle était au point vitesse orbitale nécessaire pour le faire orbiter autour de la Terre à 420 kilomètres d’altitude.
Si vous cochez en vert les trois conditions, la balle ne reviendra jamais et continuera de tomber sous l’effet de la gravité terrestre, ce qui signifie qu’elle commencera à tourner autour de la Terre.
Cela peut paraître un peu contre-intuitif, mais réfléchissez-y un peu.
La vitesse orbitale d’un objet pour qu’il tourne autour de la Terre est donnée par :
$$V_0 = \sqrt{\frac{GM_{e}}{R}}$$
Ici, $G$ est à nouveau la constante gravitationnelle, $M_{e}$ est la masse de la Terre et $R$ est la distance entre le centre de la Terre et l’objet, nous pouvons obtenir la vitesse orbitale requise pour orbiter autour du Soleil. en le remplaçant simplement par une masse du Soleil, la distance.
Et oui, une orbite n’est que le chemin suivi par cet objet lorsqu’il continue de tomber vers l’objet central mais manque la surface parce que son chemin est courbe.
Les planètes et tous les autres objets qui tournent autour du Soleil ont les vitesses orbitales requises, c’est-à-dire que lorsqu’elles sont attirées vers le Soleil, elles se déplacent également latéralement assez rapidement pour les empêcher de tomber sur le Soleil.
Mais comment les planètes obtiennent-elles leur vitesse au départ ?
D’où les planètes tirent-elles leur vitesse initiale ?
Pour répondre à cette question, nous devons nous plonger dans la « formation planétaire ».
La théorie la plus largement acceptée concernant la formation du Soleil et des planètes est qu’elle a commencé lorsqu’un nuage moléculaire géant de gaz a commencé à s’effondrer sous sa gravité.
Pour tout système stellaire de l’univers, l’étoile est la première à naître, c’est aussi pourquoi elle sera – idéalement, occupant la majeure partie de la masse – la plus massive de ce système.
Il y a Milieu interstellaire (ISM) ou simplement des nuages de gaz, répartis de manière non uniforme dans tout l’univers.
Chaque fois qu’il y a une plus grande densité de ces nuages dans une région de l’espace, en raison de la gravité de ce groupe de nuages dans cette région, il commence à se contracter et à collecter de plus en plus de masse ou de gaz provenant de l’environnement.
À mesure que le nuage de gaz se contracte, il commence à tourner en raison de la conservation du moment cinétique.
Le moment angulaire décrit le mouvement de rotation d’un objet autour d’un axe, il est le produit de sa vitesse de rotation et de sa taille, ce qui implique qu’à mesure qu’un objet se contracte, sa vitesse de rotation doit augmenter.
Cette collection devient rapidement si grande que la gravité de l’amas rassemblé commence à comprimer sa masse en un point et finit par devenir plus chaude en raison de la collision entre les molécules de gaz en contraction.
Cela conduit à la formation d’étoilesaprès la formation de l’étoile, une masse résiduelle dans le voisinage ici et là conduit à la formation de planètes et d’astéroïdes, tous avec des vitesses de rotation différentes.
Tout objet qui n’avait pas une vitesse suffisante s’est déjà écrasé sur le Soleil.
En savoir plus sur la vraie nature de la gravité : ce n’est pas vraiment une force
Jusqu’à présent, l’explication des orbites reposait sur les lois classiques de la physique utilisant les lois du mouvement et de la gravité de Newton.
Selon la théorie de la relativité générale d’Albert Einstein, les objets massifs n’attirent pas d’autres objets vers eux, ce qui signifie que la gravité n’est pas vraiment une force.
Les objets massifs déforment le tissu de l’espace-temps de telle manière que l’objet qui était censé suivre une ligne droite pour toujours dans une direction particulière semble tourner autour de cet objet.
Qu’est-ce que cela signifie?
Einstein a proposé que l’espace et le temps ne soient pas indépendants mais interconnectés l’un à l’autre et que la densité masse-énergie d’une région définit la courbure du tissu espace-temps.
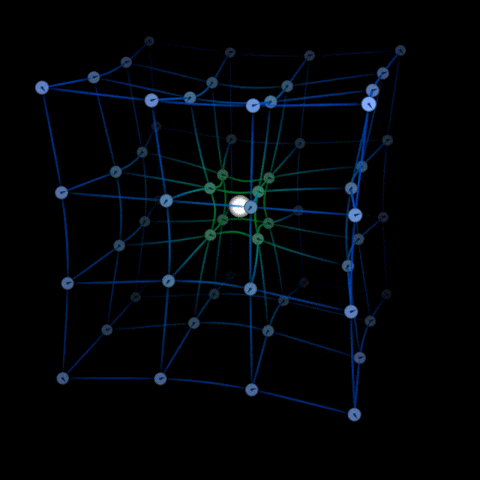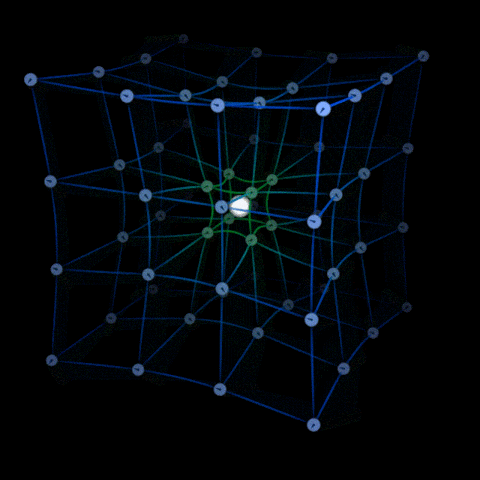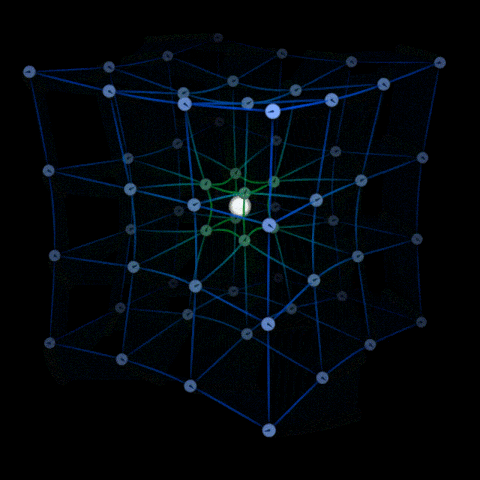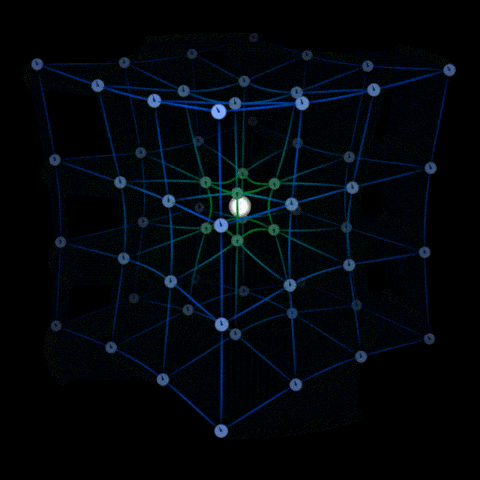

En raison de l’inertie d’un objet, il a tendance à ne pas suivre une ligne droite dans notre perspective mais se déplace simplement le long de la courbure de l’espace-temps.
Imaginez une fourmi marchant sur le papier, elle trace un chemin droit dessus.
Maintenant, pliez un peu ce papier, pour la fourmi, elle suit toujours un chemin droit, mais pour vous, elle se déplace sur un chemin courbe.
Maintenant, pliez le papier de manière à ce qu’il soit joint bout à bout. Que va-t-il se passer ?
La fourmi parcourt désormais un chemin circulaire sans avoir besoin de s’écarter de la ligne droite qu’elle suivait.
C’est ainsi que fonctionnent les orbites en relativité générale.
Et assez étrangement, il s’avère qu’aucun objet ne suivrait un chemin droit dans votre perspective à moins qu’il ne soit sous l’influence d’une autre force, mais il suit le chemin le plus court compte tenu de la courbure de l’espace-temps.
Nous appelons ce chemin géodésique, et ces chemins sont les trajectoires naturelles que les objets prendraient en l’absence de toute autre force.
Vous avez donc un corps massif courbant l’espace-temps autour de lui (c’est la gravité), pour tout autre objet à proximité, le chemin qu’il emprunte en voyageant d’un point A à B sera le plus court et le plus droit pour cet objet, bien que pour vous, en tant qu’observateur, cela n’apparaîtra pas comme une ligne droite.



